Mencari faktor persekutuan terbesar (FPB) dari 18 merupakan langkah dasar dalam matematika, khususnya aritmatika. Memahami konsep FPB dan bagaimana menemukannya untuk angka 18 sangat penting untuk menguasai berbagai konsep matematika lebih lanjut, seperti penyederhanaan pecahan, perhitungan luas dan volume, dan bahkan dalam aljabar. Artikel ini akan membahas secara detail tentang bagaimana menemukan FPB dari 18, menjelaskan berbagai metode yang dapat digunakan, dan memberikan contoh-contoh praktis agar Anda dapat memahami konsep ini dengan lebih baik.
Sebelum kita masuk ke inti pembahasan, mari kita definisikan terlebih dahulu apa itu FPB. FPB atau Faktor Persekutuan Terbesar adalah bilangan bulat terbesar yang dapat membagi habis dua atau lebih bilangan bulat lainnya tanpa sisa. Dalam kasus ini, kita akan mencari FPB dari 18. Artinya, kita akan mencari bilangan terbesar yang dapat membagi 18 tanpa meninggalkan sisa.
Salah satu metode yang paling umum digunakan untuk menemukan FPB adalah dengan menggunakan faktorisasi prima. Metode ini melibatkan memecah bilangan menjadi faktor-faktor primanya. Faktor prima adalah bilangan bulat positif yang hanya dapat dibagi habis oleh 1 dan dirinya sendiri. Mari kita terapkan metode ini untuk mencari FPB dari 18.
Metode Faktorisasi Prima untuk Mencari FPB dari 18
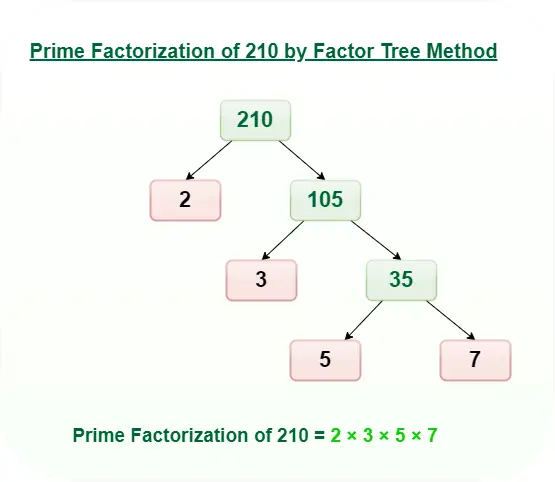
Langkah pertama adalah mencari faktor prima dari 18. Kita dapat melakukannya dengan membagi 18 secara berulang kali dengan bilangan prima terkecil sampai kita mendapatkan 1. Berikut adalah faktorisasi prima dari 18:
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Jadi, faktorisasi prima dari 18 adalah 2 x 3 x 3 atau 2 x 32. Karena 18 hanya memiliki satu bilangan itu sendiri, maka FPB dari 18 adalah 18 itu sendiri.
Sekarang, mari kita tinjau beberapa contoh tambahan untuk memperkuat pemahaman kita. Misalnya, jika kita ingin mencari FPB dari 18 dan 24, kita dapat mengikuti langkah-langkah yang sama. Pertama, kita mencari faktor prima dari kedua bilangan tersebut:
- Faktor prima dari 18: 2 x 32
- Faktor prima dari 24: 23 x 3
Kemudian, kita cari faktor-faktor prima yang sama dan pangkat terkecilnya. Dalam kasus ini, faktor prima yang sama adalah 2 dan 3. Pangkat terkecil dari 2 adalah 21 = 2, dan pangkat terkecil dari 3 adalah 31 = 3. Oleh karena itu, FPB dari 18 dan 24 adalah 2 x 3 = 6.
Metode Algoritma Euclidean
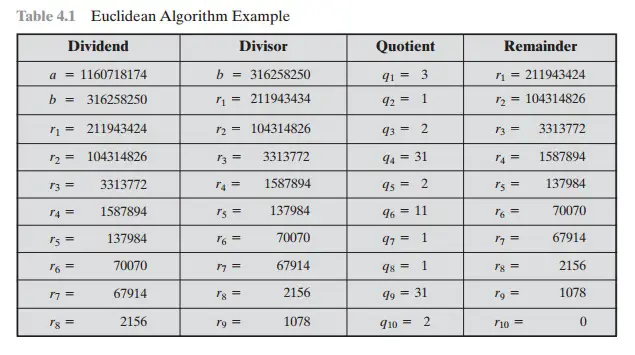
Metode lain yang dapat digunakan untuk mencari FPB adalah dengan menggunakan algoritma Euclidean. Metode ini lebih efisien untuk bilangan yang lebih besar. Algoritma Euclidean didasarkan pada prinsip bahwa FPB dari dua bilangan tidak berubah jika bilangan yang lebih besar digantikan oleh selisih antara bilangan yang lebih besar dan bilangan yang lebih kecil. Proses ini diulangi sampai kedua bilangan tersebut sama. Mari kita coba terapkan algoritma Euclidean untuk mencari FPB dari 18 dan 24:
- 24 - 18 = 6
- 18 - 6 = 12
- 12 - 6 = 6
- 6 - 6 = 0
Karena proses berhenti ketika selisihnya adalah 0, maka FPB dari 18 dan 24 adalah 6.
Untuk bilangan yang lebih besar, penggunaan algoritma Euclidean akan lebih efisien daripada metode faktorisasi prima. Namun, untuk memahami konsep FPB secara mendasar, metode faktorisasi prima lebih mudah dipahami dan divisualisasikan. Keduanya merupakan alat yang bermanfaat dalam menyelesaikan berbagai masalah matematika.
Perbandingan Metode Faktorisasi Prima dan Algoritma Euclidean
| Metode | Penjelasan | Keunggulan | Kelemahan |
|---|---|---|---|
| Faktorisasi Prima | Memecah bilangan menjadi faktor-faktor prima. | Mudah dipahami, cocok untuk bilangan kecil. | Kurang efisien untuk bilangan besar. |
| Algoritma Euclidean | Menggunakan pengurangan berulang hingga mencapai selisih 0. | Efisien untuk bilangan besar. | Lebih kompleks untuk dipahami, kurang intuitif. |
Berikut tabel yang merangkum beberapa contoh pencarian FPB:
| Bilangan | Faktor Prima | FPB |
|---|---|---|
| 18 | 2 x 32 | 18 |
| 18 dan 24 | 18: 2 x 32 24: 23 x 3 | 6 |
| 18 dan 36 | 18: 2 x 32 36: 22 x 32 | 18 |
| 18, 24, dan 36 | 18: 2 x 32 24: 23 x 3 36: 22 x 32 | 6 |
Memahami konsep FPB sangat penting dalam berbagai aplikasi matematika. Kemampuan untuk mencari FPB dengan cepat dan efisien akan sangat membantu dalam memecahkan masalah yang lebih kompleks. Dengan menguasai metode faktorisasi prima dan algoritma Euclidean, Anda akan memiliki alat yang powerful untuk menghadapi berbagai tantangan matematika.
Selain itu, pemahaman tentang FPB juga berguna dalam kehidupan sehari-hari. Bayangkan Anda memiliki 18 apel dan 24 jeruk. Anda ingin membagi buah-buahan tersebut ke dalam beberapa keranjang dengan jumlah apel dan jeruk yang sama di setiap keranjang. Berapa jumlah keranjang maksimal yang dapat Anda buat? Jawabannya adalah FPB dari 18 dan 24, yaitu 6. Anda dapat membuat 6 keranjang, masing-masing berisi 3 apel dan 4 jeruk.
Contoh lain, misalkan Anda memiliki dua lembar kertas dengan panjang 18 cm dan 24 cm. Anda ingin memotong kedua kertas tersebut menjadi potongan-potongan dengan panjang yang sama dan tanpa sisa. Berapa panjang potongan maksimal yang dapat Anda buat? Sekali lagi, jawabannya adalah FPB dari 18 dan 24, yaitu 6 cm.
Mari kita bahas lebih lanjut tentang aplikasi FPB dalam kehidupan sehari-hari. Bayangkan Anda sedang membuat kue dan Anda memiliki 18 buah strawberry dan 24 buah blueberry. Anda ingin mendekorasi kue dengan jumlah strawberry dan blueberry yang sama pada setiap potongan kue. Berapa banyak potongan kue yang dapat Anda buat?
Dengan menggunakan konsep FPB, kita dapat mencari FPB dari 18 dan 24. Seperti yang telah kita bahas sebelumnya, FPB dari 18 dan 24 adalah 6. Artinya, Anda dapat membuat 6 potongan kue, dengan masing-masing potongan kue berisi 3 buah strawberry dan 4 buah blueberry. Tidak ada sisa buah-buahan!
Contoh lain, misalnya Anda memiliki 18 pensil merah dan 24 pensil biru. Anda ingin membagi pensil-pensil tersebut ke dalam beberapa kotak dengan jumlah pensil merah dan biru yang sama di setiap kotak. Berapa banyak kotak yang dapat Anda buat? FPB dari 18 dan 24 adalah 6, jadi Anda dapat membuat 6 kotak, masing-masing berisi 3 pensil merah dan 4 pensil biru.
Konsep FPB juga sangat penting dalam bidang desain dan arsitektur. Misalnya, Anda ingin memasang ubin pada lantai dengan ukuran 18 cm x 18 cm dan 24 cm x 24 cm. Anda ingin menggunakan ubin dengan ukuran yang sama dan tanpa sisa. Ukuran ubin terbesar yang dapat digunakan adalah FPB dari 18 dan 24, yaitu 6 cm. Artinya Anda dapat menggunakan ubin dengan ukuran 6cm x 6cm.
Sekarang, mari kita jelajahi lebih dalam tentang bagaimana FPB dari 18 dapat digunakan dalam penyederhanaan pecahan. Anggaplah kita memiliki pecahan 18/36. Untuk menyederhanakan pecahan ini, kita perlu mencari FPB dari pembilang (18) dan penyebut (36). FPB dari 18 dan 36 adalah 18. Kita dapat membagi baik pembilang maupun penyebut dengan 18, sehingga menghasilkan pecahan yang paling sederhana: 18/18 = 1/2.
Contoh lain, misalnya kita memiliki pecahan 18/24. FPB dari 18 dan 24 adalah 6. Membagi pembilang dan penyebut dengan 6 menghasilkan pecahan yang paling sederhana: 18/6 = 3 dan 24/6 = 4, sehingga pecahan tersebut menjadi 3/4.
Sebagai kesimpulan, pemahaman tentang FPB, khususnya FPB dari 18 dan bagaimana cara menemukannya, merupakan kunci penting dalam berbagai aspek matematika dan aplikasi praktisnya. Baik metode faktorisasi prima maupun algoritma Euclidean memberikan cara yang efektif untuk menghitung FPB, dan pilihan metode terbaik bergantung pada kompleksitas bilangan yang terlibat. Dengan menguasai konsep ini, Anda akan memiliki fondasi yang kuat untuk memahami konsep-konsep matematika yang lebih lanjut.

Mari kita eksplorasi lebih jauh tentang konsep FPB dan bagaimana penerapannya dalam soal-soal cerita. Misalkan ada sebuah taman berbentuk persegi panjang dengan panjang 18 meter dan lebar 24 meter. Anda ingin membagi taman tersebut menjadi beberapa petak persegi yang berukuran sama besar. Berapa ukuran sisi petak persegi terbesar yang mungkin?
Jawabannya terletak pada FPB dari 18 dan 24. Seperti yang telah kita ketahui, FPB dari 18 dan 24 adalah 6. Oleh karena itu, ukuran sisi petak persegi terbesar yang mungkin adalah 6 meter. Taman tersebut dapat dibagi menjadi beberapa petak persegi dengan ukuran 6 meter x 6 meter.
Contoh lain, bayangkan Anda memiliki 18 buah apel merah dan 24 buah apel hijau. Anda ingin membuat keranjang hadiah dengan jumlah apel merah dan apel hijau yang sama di setiap keranjang. Berapa banyak keranjang yang dapat Anda buat dengan jumlah apel yang paling banyak di setiap keranjang?
Sekali lagi, kita perlu mencari FPB dari 18 dan 24, yaitu 6. Anda dapat membuat 6 keranjang, dengan masing-masing keranjang berisi 3 apel merah dan 4 apel hijau.
Dengan memahami konsep FPB dan berbagai metodenya, Anda akan mampu menyelesaikan berbagai permasalahan matematika dan kehidupan sehari-hari dengan lebih efisien dan efektif. Kemampuan untuk menentukan FPB dengan cepat dan akurat akan menjadi aset berharga dalam berbagai bidang, mulai dari matematika dasar hingga aplikasi yang lebih kompleks dalam sains dan teknik.
Ingatlah untuk selalu berlatih dan mencoba berbagai contoh soal agar pemahaman Anda tentang FPB semakin kuat. Semakin banyak Anda berlatih, semakin mahir Anda akan menjadi dalam mencari FPB dari berbagai bilangan, termasuk FPB dari 18 dan bilangan lainnya.
Sekarang, mari kita bahas lebih lanjut tentang konsep FPB dan bagaimana penerapannya dalam berbagai konteks yang lebih kompleks. Misalnya, dalam bidang kriptografi, konsep FPB digunakan dalam algoritma RSA untuk mengamankan komunikasi data. Algoritma RSA bergantung pada kesulitan memfaktorkan bilangan bulat besar menjadi faktor-faktor primanya. Kemampuan untuk menemukan FPB dengan cepat dan efisien sangat penting dalam memecahkan kode kriptografi.
Selain itu, konsep FPB juga digunakan dalam desain sirkuit elektronik. Dalam desain sirkuit digital, FPB digunakan untuk menyederhanakan ekspresi Boolean. Ekspresi Boolean adalah ekspresi yang melibatkan variabel-variabel biner (0 dan 1). Menyederhanakan ekspresi Boolean dapat mengurangi kompleksitas sirkuit dan meningkatkan efisiensi.
Lebih lanjut, FPB juga memiliki peranan penting dalam musik. Dalam teori musik, FPB digunakan untuk menentukan interval antara nada-nada musik. Interval adalah jarak antara dua nada. Interval yang harmonis seringkali didasarkan pada FPB dari frekuensi nada-nada tersebut.
Dalam ilmu komputer, FPB digunakan dalam algoritma pencarian jalur terpendek. Algoritma ini digunakan untuk menemukan jalur terpendek antara dua titik dalam sebuah graf. FPB digunakan untuk mengoptimalkan algoritma ini dan mengurangi waktu komputasi.
Di bidang rekayasa, FPB digunakan dalam desain struktur. Dalam desain struktur, FPB digunakan untuk menentukan dimensi optimal dari elemen-elemen struktur. Dimensi optimal ini membantu mengurangi berat struktur dan meningkatkan kekuatannya.
Konsep FPB juga digunakan dalam optimasi jaringan komputer. Dalam optimasi jaringan komputer, FPB digunakan untuk menentukan jalur terbaik untuk mengirimkan data. Jalur terbaik ini dapat meminimalkan latensi dan meningkatkan kecepatan transmisi data.
Selain contoh-contoh di atas, masih banyak lagi aplikasi FPB dalam berbagai bidang. Kemampuan untuk memahami dan menerapkan konsep FPB merupakan keterampilan yang sangat berharga dalam berbagai disiplin ilmu. Oleh karena itu, penting untuk memahami konsep FPB secara mendalam dan mampu menerapkannya dalam berbagai konteks.
Sebagai penutup, kita telah membahas secara detail tentang bagaimana menemukan FPB dari 18, menjelaskan berbagai metode yang dapat digunakan, dan memberikan contoh-contoh praktis dari berbagai bidang. Dengan menguasai konsep FPB, Anda akan memiliki alat yang powerful untuk menyelesaikan berbagai permasalahan matematika dan kehidupan sehari-hari dengan lebih efisien dan efektif. Ingatlah untuk terus berlatih dan memperdalam pemahaman Anda tentang konsep FPB, karena ini merupakan dasar penting dalam berbagai bidang ilmu dan teknik.
Berikut beberapa latihan soal untuk menguji pemahaman Anda tentang FPB:
- Carilah FPB dari 18 dan 30.
- Carilah FPB dari 18, 24, dan 36.
- Carilah FPB dari 18 dan 45.
- Sebuah taman berbentuk persegi panjang memiliki panjang 18 meter dan lebar 30 meter. Anda ingin membagi taman tersebut menjadi beberapa petak persegi yang berukuran sama besar. Berapa ukuran sisi petak persegi terbesar yang mungkin?
- Anda memiliki 18 pensil merah dan 30 pensil biru. Anda ingin membagi pensil-pensil tersebut ke dalam beberapa kotak dengan jumlah pensil merah dan biru yang sama di setiap kotak. Berapa banyak kotak yang dapat Anda buat?
Semoga artikel ini bermanfaat dan membantu Anda memahami konsep FPB dari 18 dan penerapannya dalam berbagai konteks.

